Parapluie de Whitney

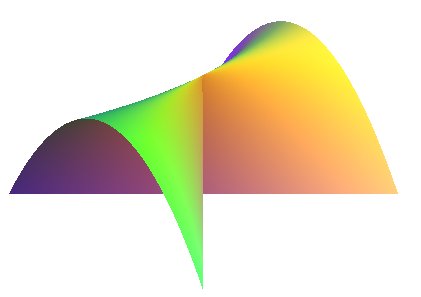
Le parapluie de Whitney est une surface présentant des auto-intersections dans l'espace ambiant de dimension 3. Elle doit son nom au mathématicien américain Hassler Whitney, qui a étudié cet objet au travers de ses travaux sur les singularités d'applications différentiables.

Formules

Les équations paramétriques de cette surface sont données en coordonnées cartésiennes par

${\displaystyle {\begin{aligned}x(u,v)&=uv\\y(u,v)&=u\\z(u,v)&=v^{2}\end{aligned}}}$

où les paramètres u et v décrivent l'ensemble des réels. Cette surface est contenue dans celle donnée par l'équation implicite :

${\displaystyle x^{2}=y^{2}z}$

mais cette dernière inclut l'axe des z (aussi appelé poignée du parapluie), alors que la représentation paramétrique impose que z soit positif.

Propriétés

Il s'agit d'un objet d'étude important en théorie des singularités. Les applications génériques opérant sur des 2-variétés et à valeurs dans R³ ne présentent que deux types de singularités stables : les lignes où se recoupent la surface et le parapluie de Whitney (plus précisément le point inférieur). On doit à Whitney lui-même cette classification.

Le parapluie de Whitney est une surface réglée et même un conoïde droit, de directrice une parabole d'axe parallèle à son axe.

Notes et références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Whitney umbrella » (voir la liste des auteurs).

Bibliographie

• Vladimir Arnold, A. Varchenko et S. Goussein-Zadé, Singularités des applications différentiables, Moscou, Mir, 1984
• (en) « Whitney's Umbrella », The Topological Zoo, The Geometry Center (consulté le 8 mars 2006) (Images and movies of the Whitney umbrella.)

• Portail de la géométrie